Introduction #

In a previous post we looked at the geometric meaning of Maxwell's equations:

∇⋅B=0;  ∇×E+∂B∂t=0, \nabla\cdot \mathbf{B}=0; \;\nabla\times \mathbf{E}+\frac{\partial \mathbf{B}}{\partial t}=0,
∇⋅E=ρϵ0;  ∇×B−ϵ0μ0∂E∂t=μ0j. \nabla\cdot \mathbf{E}=\frac{\rho}{\epsilon_0}; \; \nabla\times \mathbf{B}-\epsilon_0\mu_0\frac{\partial \mathbf{E}}{\partial t}=\mu_0\mathbf{j}.

The key thing to remember was: if you see a divergence draw a three-dimensional volume and use the divergence theorem, while if you see a curl draw a two-dimensional surface and use Stokes' theorem. We are going to use this to derive the electromagnetic boundary conditions. Hopefully by the end of this they should seem pretty intuitive, and you will be able to quickly the boundary conditions them just by looking at Maxwell's equations.

Now things are complicated by the fact that if we are not in a vacuum, the electric and magnetic fields can induce extra charges ρ\rho and currents jj in the surface, which induce new fields, which induce even more charges and currents, and so on. For this reason it is convenient to write some of the equations in terms of DD and HH, because then only the `free' charges ρf\rho_f and currents jfj_f, the ones that are put in at the start rather than induced by the fields, show up:

∇⋅B=0;  ∇×E+∂B∂t=0, \nabla\cdot \mathbf{B}=0;\;\nabla\times \mathbf{E}+\frac{\partial \mathbf{B}}{\partial t}=0,
∇⋅D=ρf;  ∇×H−∂D∂t=jf. \nabla\cdot \mathbf{D}=\rho_f;\; \nabla\times \mathbf{H}-\frac{\partial \mathbf{D}}{\partial t}=\mathbf{j}_f.

Deriving the boundary conditions #

Let's suppose we have a boundary between two media, and some sort of electromagnetic wave propagates between the two. We want to know how the fields on one side relate to the fields on the other.

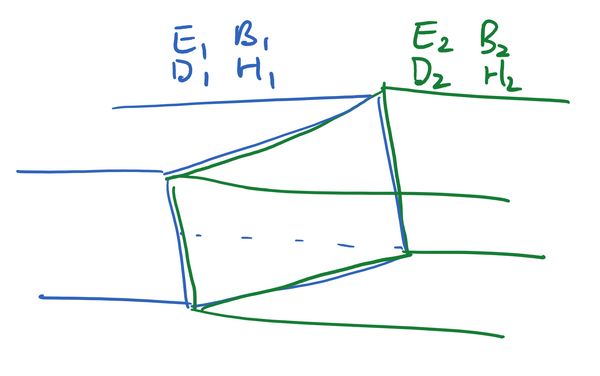
A horizontal rectangular pipe, divided at the centre. The left-hand side is coloured blue and contains the fields E1, B1, D1, H1, while the right-hand side is green with fields E2, B2, D2, H2.

We will look at the conditions imposed on the fields by each of Maxwell's laws.

Gauss' Law for the Magnetic Field #

For our first candidate we will look at

∇⋅B=0. \nabla\cdot\mathbf{B}=0.

There is a divergence, so that means we want to draw a three-dimensional box on both sides of the boundary, and use the divergence theorem to convert the left hand side to an integral of B⋅n^\mathbf{B}\cdot\hat{\mathbf{n}} over the surface.

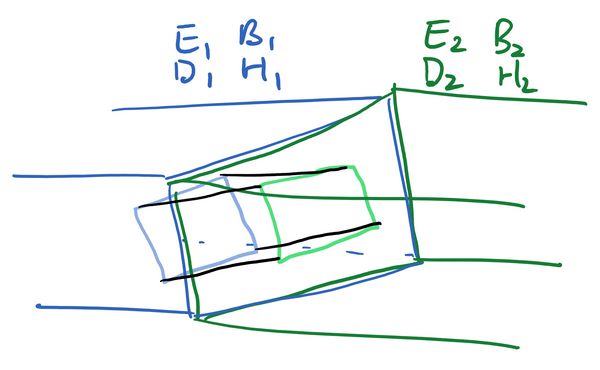
The same rectangular pipe as the previous image. Across the boundary is drawn a Gaussian pillbox (rectangular parellipiped). One face is coloured blue and just inside the left region of the pipe, parallel with the boundary. The opposite face is coloured green and inside the right region, again parallel with the boundary. The other four faces, which are perpendicular to the boundary, are coloured black.

We have a solid rectangular box. The blue face lies inside the left region, the green face inside the right region, while the black faces cross both regions. Integrating both sides of Gauss' Law gives that the integral of B⋅n^\mathbf{B}\cdot\hat{\mathbf{n}} over all six faces is equal to zero:

0=∫Blue  faceB1⋅n^+∫Green  faceB2⋅n^+∫Black  facesB⋅n^. 0=\int_{\mathrm{Blue\;face}}\mathbf{B}_1\cdot\hat{\mathbf{n}} +\int_{\mathrm{Green\;face}}\mathbf{B}_2\cdot\hat{\mathbf{n}}+\int_{\mathrm{Black\;faces}}\mathbf{B}\cdot\hat{\mathbf{n}}.

Let's suppose the blue and green faces have some area AA. Note that the unit normal n^\hat{\mathbf{n}} has opposite sign on each side of the box, so it is pointing against B1\mathbf{B}_1 but with B2\mathbf{B}_2. On the blue and green faces, taking the dot product with the unit normal selects the components of the magnetic field which are perpendicular to the boundary. We then have:

0=−∣B1⊥∣A+∣B2⊥∣A+∫Black  facesB⋅n^. 0=-|\mathbf{B}_1^{\perp}|A+|\mathbf{B}_2^{\perp}|A+\int_{\mathrm{Black\;faces}}\mathbf{B}\cdot\hat{\mathbf{n}}.

The integral over the black faces is annoying because each face has contributions from both B1B_1 and B2B_2, so it doesn't have a nice answer. We can get rid of these parts though by making the box extremely thin. We bring the blue and green face closer together, shrinking the black faces to zero area while keeping the areas of the blue and green faces at AA. With this we will have

0=−∣B1⊥∣A+∣B2⊥∣A. 0=-|\mathbf{B}_1^{\perp}|A+|\mathbf{B}_2^{\perp}|A.

Dividing through by area then gives

∣B1⊥∣=∣B2⊥∣. |\mathbf{B}_1^{\perp}|=|\mathbf{B}_2^{\perp}|.

In other words, the perpendicular component of the magnetic field is unchanged across the boundary. Since the perpendicular component of the magnetic field is B⋅n^\mathbf{B}\cdot\hat{\mathbf{n}}, another way of writing this boundary condition is

n^⋅(B2−B1)=0 \hat{\mathbf{n}}\cdot\left(\mathbf{B}_2-\mathbf{B}_1\right)=0

Gauss' Law for the Electric Field #

Now we will analyse

∇⋅D=ρf. \nabla\cdot\mathbf{D}=\rho_f.

The analysis for the left hand side is identical to what we had for the magnetic field, and we end up with

−∣D1⊥∣A+∣D2⊥∣A. -|\mathbf{D}_1^{\perp}|A+|\mathbf{D}_2^{\perp}|A.

On the right hand side however the volume integral of ρf\rho_f over the box will be equal to the enclosed free charge. Let's assume there is a charge density σf\sigma_f per unit area on the boundary, then the right hand side will be σfA\sigma_f A, and we will have

−∣D1⊥∣A+∣D2⊥∣A=σfA, -|\mathbf{D}_1^{\perp}|A+|\mathbf{D}_2^{\perp}|A=\sigma_f A,

or

−∣D1⊥∣+∣D2⊥∣=σf. -|\mathbf{D}_1^{\perp}|+|\mathbf{D}_2^{\perp}|=\sigma_f.

As before we may re-write this as

n^⋅(D2−D1)=σf. \hat{\mathbf{n}}\cdot\left(\mathbf{D}_2-\mathbf{D}_1\right)=\sigma_f.

Let's consider a special case. Suppose there is no free charge on the boundary (σf=0\sigma_f=0), and we are in linear media, so D1=ϵ1E2\mathbf{D}_1=\epsilon_1\mathbf{E}_2 and D2=ϵ2E2\mathbf{D}_2=\epsilon_2\mathbf{E}_2. In this case the boundary condition becomes:

n^⋅(ϵ2E2−ϵ1E1)=0, \hat{\mathbf{n}}\cdot\left(\epsilon_2\mathbf{E}_2-\epsilon_1\mathbf{E}_1\right)=0,

and we see that the normal component of the electric field is discontinuous across the boundary. The intuition for this is that the electric fields induce a bound charge density on the boundary, which causes the normal component of the electric fields to be discontinuous.

Faraday's Law #

We're done with the divergences, so let's move onto the simpler one of the curl equations:

∇×E=−∂B∂t. \nabla\times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}.

Since we have a curl, this time we will draw a two-dimensional surface and then use Stokes' theorem.

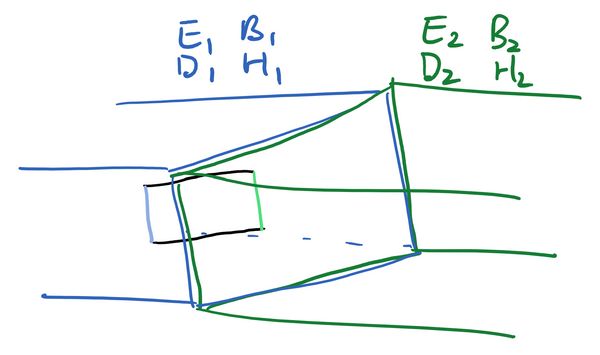
The rectangular pipe, but instead of the pillbox we have a rectangle whose face is perpendicular to the boundary. The left-hand side is parallel to the boundary, inside the left-hand region, and coloured blue. The right-hand side is also parallel to the boundary, inside the right-hand region, and coloured green. The top and bottom sides are perpendicular to the boundary and coloured black.

Now the blue line lies inside the left material, the green line inside the right material, and the black lines cross the boundary and lie in both materials. We integrate both sides of Faraday's law over this surface. For the left hand side Stokes' theorem converts the integral of the curl over this surface to the line integral around the boundary:

∫Blue  lineE1⋅dl+∫Green  lineE2⋅dl+∫Black  linesE⋅dl. \int_{\mathrm{Blue\;line}}\mathbf{E}_1\cdot d\mathbf{l} +\int_{\mathrm{Green\;line}}\mathbf{E}_2\cdot d\mathbf{l}+ \int_{\mathrm{Black\;lines}}\mathbf{E}\cdot d\mathbf{l}.

Suppose the blue and green lines have length ll, then the line integrals over these become the parallel component of E\mathbf{E} multiplied by ll, with again a sign difference because the line integral is pointing down on the blue side and up on the green side (as it goes anticlockwise around the rectangle)

=∣E1∥∣l−∣E2∥∣l+∫Black  linesE⋅dl. =|\mathbf{E}_1^{\parallel}|l-|\mathbf{E}_2^{\parallel}|l+ \int_{\mathrm{Black\;lines}}\mathbf{E}\cdot d\mathbf{l}.

Again the integrals over the black line are annoying, as each line crosses between the two regions. But again the cure is the same, to move the blue and green lines closer together (keeping them at length ll), squeezing the rectangle thinner and thinner until the lengths of the black lines go to zero. In this case the integral over the black lines vanishes and we have

=∣E1∥∣l−∣E2∥∣l =|\mathbf{E}_1^{\parallel}|l-|\mathbf{E}_2^{\parallel}|l

For the right hand side we want to integrate −∂tB-\partial_t\mathbf{B} over the face of the rectangle. However we just squeezed the rectangle infinitely thin, so we will be integrating this over zero area, which will give us zero. The net result is

∣E1∥∣l−∣E2∥∣l=0, |\mathbf{E}_1^{\parallel}|l-|\mathbf{E}_2^{\parallel}|l=0,

and then dividing by ll we find that the parallel component of the electric field is continuous across the boundary. Since the parallel component is the part perpendicular to the normal vector, we can also write this as

n^×(E1−E2)=0. \hat{\mathbf{n}}\times\left(\mathbf{E}_1-\mathbf{E}_2\right)=0.

Ampère's Law #

This one is left as an exercise to the reader! Begin with

∇×H=j+∂D∂t, \nabla\times \mathbf{H}=\mathbf{j}+\frac{\partial\mathbf{D}}{\partial t},

and show that you end up with

n^×(H2−H1)=js \hat{\mathbf{n}}\times\left(\mathbf{H}_2-\mathbf{H}_1\right)=\mathbf{j}_s

where js\mathbf{j}_s is the surface current density. If there is no free current and we are in a linear material (B=μH\mathbf{B}=\mu\mathbf{H}), this becomes

n^×(1μ2B2−1μ1B1)=0.\hat{\mathbf{n}}\times\left(\frac{1}{\mu_2}\mathbf{B}_2-\frac{1}{\mu_1}\mathbf{B}_1\right)=0.

Conclusion #

There you have it! Once you understand the general principle, you can read off the boundary conditions very quickly by just looking at Maxwell's laws:

∇⋅B=0;  ∇×E+∂B∂t=0, \nabla\cdot \mathbf{B}=0;\;\nabla\times \mathbf{E}+\frac{\partial \mathbf{B}}{\partial t}=0,
∇⋅E=ρϵ0;  ∇×B−ϵ0μ0∂E∂t=μ0j. \nabla\cdot \mathbf{E}=\frac{\rho}{\epsilon_0};\; \nabla\times \mathbf{B}-\epsilon_0\mu_0\frac{\partial \mathbf{E}}{\partial t}=\mu_0\mathbf{j}.

The divergence laws will tell you about the perpendicular components, while the curl laws tell you about the parallel. The homogenous (source-free) laws give you continuity (the same fields on either side), while the inhomogeneous laws lead to discontinuity (factors of μ\mu and ϵ\epsilon on either side). After a bit of thinking you should be able to jump straight to
n^⋅(B2−B1)=0;  n^×(E1−E2)=0, \hat{\mathbf{n}}\cdot\left(\mathbf{B}_2-\mathbf{B}_1\right)=0;\; \hat{\mathbf{n}}\times\left(\mathbf{E}_1-\mathbf{E}_2\right)=0,
n^⋅(D2−D1)=σf;  n^×(H2−H1)=js.\hat{\mathbf{n}}\cdot\left(\mathbf{D}_2-\mathbf{D}_1\right)=\sigma_f;\;\hat{\mathbf{n}}\times\left(\mathbf{H}_2-\mathbf{H}_1\right)=\mathbf{j}_s.