Introduction #
Let's take a look at Maxwell's equations (in differential form):
We'll try and understand what these mean geometrically, and how you can go about using them.
Some Vector Calculus #
Firstly we need some vector calculus. Let's start off with some vector field . The divergence of is given by
What does the divergence mean intuitively? Imagine placing a tiny sphere at some point , and letting the surface of the sphere be pushed and pulled by the vector field . Depending on the vector field the surface of the sphere will be distorted, and its volume will change. The rate of change of volume is given by the divergence of at . If the divergence is positive, that means the volume of the sphere will increase. If the divergence is negative, then the volume of the sphere will decrease. If the divergence is zero then the shape of the sphere may be distorted, but in such a way that the volume remains constant.
The divergence is related to the divergence theorem. Let be some solid volume, its surface, and the normal vector. For if were the solid ball of radius , then would be the surface of that ball, namely the sphere of radius , and the unit normal vector on the sphere. The divergence theorem relates the integral of the divergence of over , with the integral of over the surface of :
Imagine an incompressible fluid in three dimensions, being pushed around by . If the divergence is positive at a point then fluid is being created and pushed outwards. If the divergence is negative then the fluid is being sucked away, while if the divergence is zero then the vector field is pushing the fluid around, without creating or destroying it. The left hand side of the equation above is the sum over the entire volume of how much fluid is being created or sucked up. Now let's look at the right hand side. The dot product asks how much fluid is being pushed through the boundary; if the dot product is positive then fluid is being pushed out of the surface, if the dot product is negative then fluid is being pushed into the surface, while if the dot product is zero then fluid is circulating around the surface, without going inwards or outwards.
In other words the divergence theorem says that the sum of all the fluid being created or sucked up at each point in the entire volume is equal to the net amount of fluid that gets pushed into or out of the surface.
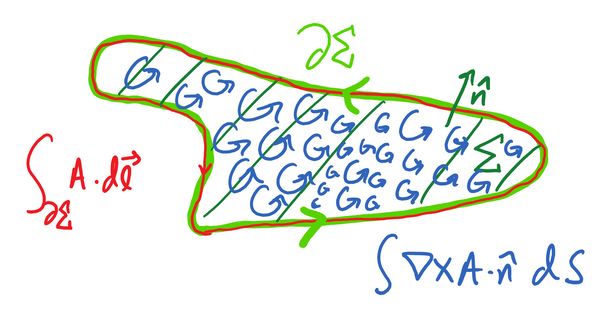
Next we have the curl:
To interpret the curl, imagine placing a tiny sphere at some point , but fix it in place so that it cannot move. Let's suppose this sphere is rigid, so that it's surface cannot be stretched. You can imagine at each point on the surface of the sphere giving it a little push or pull. If we let all these pushes and pulls add up, the sphere will start to rotate. The magnitude of the curl tells you how fast the sphere will rotate due to its surface being pushed by , and the direction of the curl tells you the axis the sphere will rotate around.
The curl is related to Stokes' theorem. Let be a two-dimensional solid region with normal vector , and the one-dimensional boundary of . Stokes' theorem relates the integral of the curl over to the line integral of around the boundary:
The left hand side gives the integral over of the circulation of the vector field in the plane of . The right hand side gives the net circulation of around the boundary.
Stokes' theorem says that the sum of circulation of fluid at every point of a two-dimensional surface is equal to the net circulation around the boundary of the surface.
The Meaning of Maxwell's Equations #
Armed with our knowledge of vector calculus, let's take another look at Maxwell's equations. We'll begin with the divergence of the magnetic field:
This equation says that there are no 'sources' or 'sinks' of the magnetic field lines. The magnetic field is neither created nor destroyed, it just flows from one place to another. If you draw a solid region, there is just as much magnetic field coming into the region as coming out. Things are slightly different for the electric field however:
If there is no charge in a region of space, then electric field lines are also neither created nor destroyed. If you have positive charge however this acts as a source of electric field lines, and a region enclosing positive charge will on the whole have electric field being 'produced' inside and flowing outwards from the surface. Negative charge on the other hand acts as a sink, 'sucking in' the electric field. If you consider a region enclosing negative charge, the electric field will flow inwards through the boundary.
The moral of the story is every time you see a divergence in Maxwell's equations, imagine drawing a three-dimensional volume and use the divergence theorem to convert this to an integral of over the surface.
Similarly every time you see a curl in Maxwell's equations, draw a two-dimensional surface and use Stokes' theorem to convert this to an integral of around the boundary.
Let's see this with Faraday's law:
Integrate both sides of this over a two-dimensional surface. The right hand side will be the rate of change of the flux of through the surface. If the flux is changing, this will induce an electric field circulating around the boundary of this surface. The case is similar for
only now we find that a current also induces a circulating magnetic field around the boundary.